ABSTRAK
Sifat molekular dalam simulasi gabungan mekanika kuantum dan mekanika molekular (QM/MM) telah terbukti bergantung pada ukuran daerah mekanika kuantum (QM) dan jumlah pengambilan sampel konformasi. Penelitian sebelumnya sebagian besar berfokus pada sistem enzimatik, yang membuatnya sulit untuk membedakan efek ukuran daerah QM dan pengambilan sampel konformasi dari faktor-faktor lain termasuk artefak batas QM-MM dan efek batas. Penelitian ini menggunakan metode solvasi adaptif berbasis perbedaan QM/MM untuk menyelidiki reaksi tautomerisasi alanin dan aspartat dalam pelarut eksplisit. Pilihan sistem yang dapat ditangani secara komputasi memungkinkan pemisahan efek ukuran daerah QM dari faktor-faktor lain dan perbandingan langsung permukaan energi bebas dengan permukaan energi potensial (PES). Hasil penelitian menunjukkan bahwa (1) sangat penting untuk memperhitungkan fluktuasi termal di sepanjang jalur reaksi dengan tepat, dan (2) permukaan energi bebas menyatu dengan cepat dengan meningkatnya ukuran daerah QM, sedangkan transfer muatan memerlukan daerah QM yang sedikit lebih besar untuk mencapai konvergensi. Temuan-temuan ini diharapkan dapat memandu penelitian masa depan mengenai sistem enzimatik dan sistem kompleks lainnya di mana metode QM/MM diterapkan.

1 Pendahuluan
Di antara faktor-faktor perdebatan berkelanjutan dalam literatur tentang sensitivitas simulasi mekanika kuantum dan mekanika molekuler (QM/MM) hibrida [ 1 – 3 ] adalah (1) bagaimana derajat pengambilan sampel konformasi mempengaruhi keakuratan sifat-sifat energetik [ 4 – 6 ] dan (2) ukuran wilayah QM yang diperlukan untuk deskripsi konvergen fenomena yang dimaksud [ 7 , 8 ]. Melakukan simulasi QM/MM dengan deskripsi korelasi elektron ab initio dari wilayah QM dan pengambilan sampel konformasi yang cukup membutuhkan komputasi intensif untuk reaksi enzimatik [ 9 – 11 ]. Seringkali, untuk mengurangi biaya, wilayah QM dimodelkan dengan teori fungsional kerapatan (DFT) [ 12 ] atau pendekatan semiempiris [ 13 ], dan simulasi QM/MM dilakukan dengan meminimalkan energi pada permukaan energi potensial (PES) QM/MM, yaitu, mengabaikan efek energi termal dan titik nol [ 7 , 9 ]. telah menunjukkan secara meyakinkan bahwa untuk reaksi hipotetis ion metafosfat dengan air dalam kompleks Ras•GAP, hasil berdasarkan pendekatan minimisasi energi QM/MM sangat sensitif terhadap pilihan konfigurasi awal (yaitu, minimum energi lokal) terutama ketika kompleks reaktan memiliki beberapa minima yang dapat diakses secara termodinamika dan kinetik [ 4 ].

Satu cara yang mungkin untuk mengatasi keterbatasan tersebut adalah dengan melakukan perhitungan minimisasi energi QM/MM pada sejumlah besar struktur yang diambil sampelnya dari simulasi MM atau QM/MM klasik [ 14 ]. Namun, tidak mudah untuk langsung membandingkan data yang dihitung dengan data eksperimen. Lebih jauh, Riccardi et al. menunjukkan dengan sistem model, transfer proton jarak jauh dalam karbonik anhidrase, bahwa hambatan reaksi dan energi yang berbeda diperoleh dengan minimisasi energi yang dimulai dari keadaan reaktan yang diambil sampelnya dari QM/MM, keadaan transisi, atau keadaan produk, meskipun menggunakan sejumlah besar struktur [ 5 ]. Dihipotesiskan bahwa lingkungan lebih suka menstabilkan keadaan kimia yang dipilih, dan bahwa perhitungan tersebut tidak dapat menangkap energi reorganisasi protein di sepanjang jalur reaksi [ 15 ]. Pekerjaan terbaru oleh Kulik dan rekan kerja mengonfirmasi bahwa energi penghilangan Zn 2+ di situs pengikatan Zn 2+ dari DNA metiltransferase 1 menunjukkan variasi besar tergantung pada konfigurasi yang diambil sampelnya [ 6 ]. Demikian pula, jebakan serupa dalam simulasi klasik telah ditunjukkan pada selektivitas ion [ 16 ], dan disimpulkan bahwa fluktuasi termal dan efek entropi harus disertakan dalam studi komputasi.

Di sisi lain, ketergantungan ukuran daerah QM telah dibahas secara luas dalam literatur [ 17 – 23 ]. Misalnya, telah ditunjukkan dalam reaksi transfer metil dari S -adenosil metionina ke katekolat yang dikatalisis oleh katekol- O -metiltransferase (COMT) bahwa sifat-sifat yang diinginkan hanya konvergen dengan sejumlah besar residu protein (hingga 500 atom) berdasarkan minimisasi energi QM/MM dengan deskripsi DFT dari daerah QM struktur yang diambil sampelnya dari simulasi dinamika molekuler klasik [ 6 , 7 , 24 ]. Sebaliknya, Jindal dan Warshel menunjukkan bahwa untuk sistem yang sama dengan deskripsi PM6/MM, hambatan energi bebas dari simulasi potensi gaya rata-rata (PMF) relatif tidak sensitif terhadap ukuran daerah QM, asalkan residu yang bersentuhan langsung disertakan dalam daerah QM [ 8 ]. Demikian pula, Demapan et al. menemukan bahwa keseimbangan utama, kinetik, dan sifat struktur elektronik untuk transfer metil dalam COMT menunjukkan variasi terbatas sehubungan dengan ukuran wilayah QM dalam simulasi DFTB3/MM mereka. Mereka menyimpulkan bahwa beberapa detail simulasi, seperti konformasi enzim awal yang berbeda, kondisi batas, dan skema partisi QM/MM, menentukan hasil simulasi enzim QM/MM dengan kontribusi yang sebanding, dan sangat penting untuk mengkalibrasi metode QM/MM untuk sistem tertentu yang diminati [ 25 ].

Pekerjaan sebelumnya yang menyelidiki efek pengambilan sampel konformasi dan ukuran wilayah QM sebagian besar difokuskan pada reaksi enzimatik [ 25 – 27 ]. Chen et al. menggunakan reaksi model yang jauh lebih mudah ditangani, reaksi tautomerisasi (netral menjadi zwitterion) asam amino dalam gugus air besar, untuk menilai secara sistematis keakuratan model QM/MM [ 1 , 28 , 29 ]. Pilihan sistem ini menghindari komplikasi yang timbul dari penggunaan skema yang berbeda untuk menangani batas QM-MM (misalnya, atom penghubung versus orbital hibrida umum) [ 1 , 28 , 30 ] dan memungkinkan perbandingan langsung antara penanganan QM penuh dan perhitungan QM/MM. Penelitian ini mengungkap beberapa temuan yang mengejutkan termasuk (1) perlunya ukuran wilayah QM yang relatif besar (30 atau lebih air yang mengelilingi asam amino) agar energi reaksi QM/MM dan hambatan dapat bertemu dalam 1,4 kkal/mol dari patokan QM langsung, dan (2) penggunaan QM semiempiris atas potensi penanaman MM muatan tetap tidak selalu mempercepat konvergensi ukuran wilayah QM.

Dalam karya ini, kami akan membahas efek pengambilan sampel konformasi dan ukuran wilayah QM menggunakan reaksi tautomerisasi alanin (Ala) dan aspartat (Asp) dengan DFTB3/MM [ 5 , 31 ]. Selain keuntungan yang disebutkan di atas, pilihan sistem dan metode memungkinkan kita untuk (1) langsung membandingkan sifat reaksi berdasarkan perhitungan energi bebas dengan yang berdasarkan minimisasi energi dan (2) memantau konvergensi permukaan energi bebas sebagai fungsi dari ukuran wilayah QM. Reaksi tautomerisasi asam amino dalam air melibatkan satu kesulitan teknis dalam simulasi QM/MM konvensional; yaitu bagaimana memodelkan molekul pelarut difusif dengan benar di sekitar zat terlarut QM [ 12 , 32 , 33 ]. Kami akan menggunakan metode QM/MM adaptif [ 34 ] yang diimplementasikan dalam Amber, di mana wilayah QM secara otomatis diperbarui berdasarkan kedekatan dengan zat terlarut QM. Pekerjaan saat ini menunjukkan bahwa hambatan reaksi dan energi reaksi dari simulasi PMF menunjukkan variasi terbatas dengan ukuran wilayah QM yang berbeda. Hal ini menggembirakan untuk simulasi QM/MM katalisis enzim yang dalam praktiknya mungkin cukup untuk menyertakan wilayah langsung di sekitar atom yang bereaksi. Sebaliknya, variasi signifikan diamati untuk perhitungan berbasis minimisasi energi, dan perhitungan tersebut tanpa pengambilan sampel konformasi yang tepat dapat menyebabkan kesalahan substansial. Makalah ini disusun sebagai berikut. Rincian komputasi akan dijelaskan di Bagian 2 , diikuti oleh Hasil dan Diskusi. Kesimpulan akan diambil di Bagian 4 .

2 Metode
Deskripsi dan Persiapan Sistem
Studi ini berfokus pada reaksi tautomerisasi (zwitterion menjadi netral) asam amino dalam pelarut eksplisit. Model DFTB3 (set parameter 3ob) [ 31 , 35 ] dipilih sebagai model QM, dan medan gaya CHARMM36m [ 36 ] digunakan untuk teori level MM untuk asam amino. Tiga sistem disiapkan menggunakan server CHARMM-GUI [ 37 , 38 ] yang pertama adalah molekul alanin yang disolvasi dengan 2014 air TIP3P dalam kotak kubik periodik dengan panjang tepi 40 Å, yang kedua adalah molekul alanin yang disolvasi dengan 3906 air TIP3P dalam kotak kubik periodik dengan panjang tepi 50 Å, dan yang ketiga adalah aspartat dengan rantai samping terdeprotonasi yang disolvasi dengan 3905 air TIP3P dalam kotak kubik periodik dengan panjang tepi 50 Å. Sel periodik yang mengandung Asp tidak dinetralkan dengan ion lawan.

2.1 Simulasi Dinamika Molekuler
Tiga jenis simulasi yang berbeda dilakukan: simulasi MM, simulasi QM/MM konvensional (cQM/MM), dan simulasi adaptif berbasis perbedaan (adQM/MM) (Tabel S1 ). Dalam simulasi cQM/MM, hanya atom terlarut yang diperlakukan secara mekanika kuantum. Dalam simulasi adQM/MM, kulit solvasi tambahan diperlakukan secara mekanika kuantum baik di wilayah yang disebut aktif (A) atau wilayah transisi (T). Di wilayah A, atom diperlakukan dengan deskripsi QM penuh, dan di wilayah T, atom menampilkan “karakter” QM dan MM yang dikombinasikan dengan lancar menggunakan algoritma interpolasi. Sistem Ala 40 Å digunakan untuk pekerjaan awal yang melibatkan simulasi MM, QM/MM konvensional (cQM/MM), dan MD adQM/MM X , di mana adQM/MM X merujuk pada ukuran wilayah QM (delapan molekul air di wilayah A, 16 molekul air di wilayah T) yang awalnya dipilih untuk menilai perbedaan dalam struktur solvasi dengan peningkatan ukuran wilayah QM. Sistem Ala 50 Å digunakan untuk simulasi PES cQM/MM dan simulasi pengambilan sampel dan pembobotan ulang payung (PMF) serta simulasi PMF adQM/MM, dan sistem Asp 50 Å digunakan untuk semua simulasi Asp.

Dalam simulasi adQM/MM, pusat wilayah QM ditetapkan ke C α dari asam amino, dan ukuran wilayah QM ditingkatkan secara sistematis dengan memasukkan lebih banyak cangkang solvasi ke wilayah A dan cangkang solvasi berikutnya ke wilayah T. Cangkang solvasi ditetapkan berdasarkan lintasan cQM/MM. Untuk sistem alanin, total dua sistem adQM/MM dipertimbangkan. Untuk sistem pertama (adQM/MM(1)), wilayah A berisi cangkang solvasi pertama, dan wilayah T berisi cangkang solvasi kedua. Untuk sistem kedua (adQM/MM(2)), wilayah A berisi cangkang solvasi pertama dan kedua, dan wilayah T berisi cangkang solvasi ketiga. Untuk sistem aspartat, selain sistem adQM/MM yang disebutkan di atas, dua sistem adQM/MM(2*) dan (3*) juga dibangun. Rincian lebih lanjut disediakan di bagian Hasil dan Pembahasan yang relevan. Semua sistem pertama-tama direlaksasi dengan 5000 langkah minimisasi energi, diikuti oleh 125 ps keseimbangan dalam ensembel NVT. Sebanyak 1 μs dalam ensembel NPT diambil sampelnya pada level teori MM dan cQM/MM, dan 25 ns NPT diambil sampelnya dengan skema partisi adQM/MM X , di mana 8 air pelarut berada di wilayah aktif dan 16 air berada di wilayah transisi. Asam amino ditahan di pusat kotak periodik dengan potensi penahanan harmonik posisional pada Cα dengan konstanta gaya 5 kkal mol −1  Å −2 . Langkah waktu integrasi 1 fs digunakan untuk simulasi dinamika MM dan cQM/MM, dan ini dikurangi menjadi langkah waktu 0,5 fs untuk semua simulasi yang menggunakan metode adQM/MM. Termostat Langevin [ 39 , 40 ] digunakan untuk mempertahankan suhu konstan pada 303,15 K, dan koefisien gesekan ditetapkan pada 1 ps −1 untuk simulasi MM dan cQM/MM dan 5 ps −1 untuk simulasi adQM/MM. Barostat Monte Carlo [ 41 ] digunakan untuk mempertahankan tekanan konstan 1 bar. Interaksi elektrostatik jarak jauh dihitung dengan algoritma particle-mesh-Ewald (PME), dan interaksi jarak jauh dipotong pada 12 Å dengan fungsi pengalihan halus diterapkan pada 10 Å. Algoritma SHAKE [ 42 ] digunakan untuk membatasi semua ikatan MM yang melibatkan atom hidrogen dalam simulasi cQM/MM dan adQM/MM.

2.2 Simulasi PES
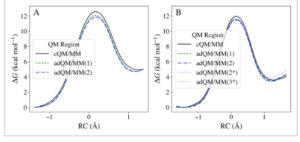
Metode penggerak koordinat digunakan untuk menentukan jalur energi minimum (MEP) yang mungkin untuk setiap 10 replikasi dari setiap sistem [ 43 ]. Ini melibatkan definisi koordinat reaksi (RC) dari reaksi tautomerik untuk setiap replikasi dalam bentuk RC = d N–H —d O–H (Gambar 1 ). Atom oksigen dipilih dari kumpulan atom oksigen di terminal C, dan atom hidrogen dipilih dari kumpulan atom hidrogen di terminal N; identitas atom H dan O bergantung pada pasangan mana yang memiliki jarak minimum dalam struktur tempat metode penggerak koordinat akan dimulai. Pengekangan yang terkait dengan RC ini kemudian mengambil bentuk E res  =  k (d N–H —d O–H ) [ 2 ]. Gaya pengekangan k ditetapkan pada 500,0 kkal mol −1  Å −2 dan interval dalam RC ditetapkan pada 0,1 Å. Nilai RC adalah sebagai berikut: Ala: −1,4 Å ≤ RC ≤ 1,4 Å; Asp: −1,7 Å ≤ RC ≤ 1,7 Å dengan langkah 0,1 Å. Metode PES mencakup total 20 pemindaian maju dan mundur.
GAMBAR 1
Buka di penampil gambar
Kekuatan Gambar
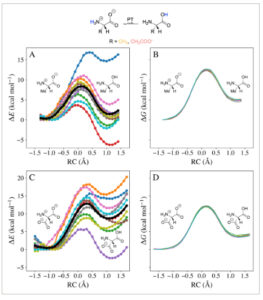
Perbandingan profil reaksi PES (A, C) dan PMF (B, D) untuk reaksi tautomerisasi cQM/MM dari alanin (A, B) dan aspartat (C, D). Setiap subplot berisi profil reaksi untuk sepuluh replikasi. Subplot (A) dan (C) menunjukkan profil reaksi PES yang terkonvergensi (setelah 20 pemindaian maju dan mundur RC) dan rata-rata dari sepuluh replikasi ditunjukkan dalam warna hitam. Subplot (B, D) menunjukkan profil reaksi PMF yang terkonvergensi. Koordinat reaksi RC didefinisikan sebagai berikut: RC = d N–H —d O–H .

2.3 Simulasi PMF
Profil energi bebas dari reaksi tautomerik dihitung dalam pelarut eksplisit. Semua simulasi dilakukan pada suhu 303,15 K dan tekanan 1 bar. Kurva PMF dihitung menggunakan metode pengambilan sampel payung sepanjang RC yang sama yang digunakan untuk simulasi PES. Rentang yang sama untuk RC digunakan untuk metode pengambilan sampel payung seperti metode PES (29 jendela untuk Ala, 35 jendela untuk Asp). Struktur untuk setiap jendela adalah nilai RC dari lintasan terakhir RC selama simulasi PES, yang menghasilkan 10 replikasi untuk setiap asam amino yang dipertimbangkan. Potensial pengekang bias harmonik diterapkan pada RC, dan konstanta gaya ditetapkan ke k  = 50 kkal mol −1  Å −2 . Bergantung pada ukuran wilayah QM, protokol ekuilibrasi dan produksi berbeda: simulasi cQM/MM dan adQM/MM(1) melibatkan ekuilibrasi 20 ps dalam ansambel NVT diikuti oleh 40 ps MD produksi NPT. Karena biaya, ekuilibrasi adQM/MM(2), (2*), (3*) diunggulkan dengan struktur akhir jendela adQM/MM(1) yang diseimbangkan, dan ekuilibrasi 2 ps dalam ansambel NVT diikuti oleh produksi NPT 10 ps dilakukan. Untuk semua simulasi pengambilan sampel payung, algoritma WHAM [ 44 , 45 ] digunakan untuk merekonstruksi PMF sepanjang RC dari data simulasi yang bias.

2.4 Analisis Transfer Muatan
Kami menyelidiki ketergantungan ukuran QM dari transfer muatan antara zat terlarut QM dan pelarut QM. Pertama, struktur solvasi di sekitar sistem alanin dan aspartat ditentukan pada tingkat cQM/MM. Seribu struktur diambil dari simulasi MD cQM/MM 1 μs dari alanin dan aspartat. Untuk setiap struktur, kami memilih set molekul air tertentu yang memungkinkan transfer muatan. Kami menyebut set ini QMR0 , QMR1 , QMR2 , dan QMR3 . Untuk QMR0 , tidak ada transfer muatan ke lingkungan sekitar yang diizinkan; artinya, semua molekul air dikeluarkan dari wilayah QM. n molekul air terdekat [molekul dengan d( Cα – Osolv ) terendah ] yang ditemukan berada di kulit solvasi pertama melalui analisis fungsi distribusi radial (RDF) ditambahkan ke QMR0 , dan ini membentuk QMR1 . Demikian pula, untuk QMR 2 , QMR 3 , dst., molekul pelarut tambahan yang termasuk dalam cangkang solvasi yang berurutan ditambahkan ke wilayah QM. Perhitungan titik tunggal QM/MM konvensional kemudian dilakukan untuk 1.000 struktur tersebut di mana wilayah QM hanya mengandung zat terlarut (QMR 0 ), zat terlarut dan cangkang solvasi pertama (QMR 1 ), zat terlarut, cangkang solvasi pertama, dan cangkang solvasi kedua (QMR 2 ), dst., dan muatan Mulliken dihasilkan dari perhitungan titik tunggal cQM/MM ini. Muatan Mulliken digunakan karena penanaman elektronik dalam DFTB3/MM didasarkan pada muatan Mulliken [ 46 , 47 ] dan penelitian sebelumnya telah menunjukkan bahwa analisis Mulliken dengan DFTB3/MM secara umum konsisten dengan hasil DFT/MM tingkat tinggi berdasarkan muatan CM5 [ 25 ]. Selain itu, QUICK [ 48 – 52 ] /MM yang diterapkan di Amber22 digunakan untuk perhitungan titik tunggal untuk analisis muatan Mulliken dengan metode B3LYP [ 53 – 56 ] /6-31G* [ 57 – 59 ].
Semua simulasi dilakukan menggunakan Amber22 [ 60 ], analisis RDF lintasan dilakukan dengan VMD [ 61 ], dan semua analisis lintasan lainnya dilakukan menggunakan MDAnalysis.

3 Hasil dan Pembahasan
3.1 Perbandingan Antara PES dan PMF (cQM/MM)
Untuk menyelidiki pentingnya pengambilan sampel konformasi, kami memeriksa tingkat variabilitas energik dalam simulasi PES dan PMF. Untuk melakukannya, kami menggunakan metode cQM/MM dalam pemeriksaan reaksi model dengan pelarut eksplisit. Di sini, kami telah mempertimbangkan 10 replikasi, yang diambil dari simulasi cQM/MM, dari sistem alanin dan aspartat untuk memeriksa konvergensi hambatan energi aktivasi (bebas) dan energi reaksi (bebas).

Metode PES yang digunakan dalam pekerjaan ini menghasilkan kesimpulan yang sesuai dengan pekerjaan sebelumnya dalam sistem enzimatik [ 4 – 6 ]; energetika potensial sangat bergantung pada struktur awal. Meskipun struktur awal asam amino dalam replikasi yang berbeda sangat mirip (Tabel S2 ), PES memiliki variasi substansial (Gambar 1A, C , Tabel 1 , Gambar S1 ). Energi aktivasi dan reaksi menunjukkan rentang yang luas di 10 replikasi setiap sistem; rentang terkecil untuk penghalang aktivasi maju dan energi reaksi adalah aspartat pada 12,5 dan 17,8 kkal mol −1 , masing-masing (Gambar 1A, C dan Tabel 1 ). Rentang ini tidak mewakili outlier, karena deviasi standar juga cukup besar; deviasi standar terkecil yang terlihat adalah untuk penghalang aktivasi maju alanin, yaitu σ  = 3,6 kkal mol −1 . Meskipun ukuran sistem reaktifnya kecil, kami mengamati bahwa minimisasi energi QM/MM mengalami ketergantungan konformasi yang sama terhadap energi potensial yang diketahui menjadi karakteristik sistem protein fleksibel [ 16 ] (Gambar S1 ). Dengan demikian, metode PES bukanlah metode mandiri yang baik untuk mendapatkan energi yang konsisten, bahkan untuk sistem model ini.

TABEL 1. Statistik ringkasan energetika (bebas) dalam kkal/mol dalam simulasi PES dan PMF a .
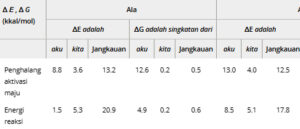Untuk metode PMF, struktur awal dari pemindaian mundur akhir semua replikasi PES digunakan sebagai struktur awal. Profil energi bebas cQM/MM menunjukkan rentang nilai yang sangat sempit (dalam 1 kkal mol −1 ) untuk Δ G a dan Δ G rxn (Gambar 1B,D dan Tabel 1 ). Terlepas dari struktur awal yang digunakan, metode PMF menghasilkan hasil yang konsisten, dan simpangan baku untuk energi bebas aktivasi dan reaksi kurang dari atau sama dengan 0,2 kkal mol −1 . Untuk sistem model yang dipelajari di sini, biaya komputasi untuk mencapai PES dan PMF yang konvergen sebanding (Tabel S3 dan Gambar S2 ). Ini menunjukkan bahwa perhitungan PMF adalah pendekatan yang andal untuk mendapatkan energi reaksi berdasarkan simulasi QM/MM.

Dalam penelitian ini, kami berfokus pada mekanisme transfer proton intramolekuler. Namun, penting untuk mengakui bahwa molekul air di sekitarnya juga dapat berperan dalam memfasilitasi tautomerisasi melalui transfer proton yang dibantu air. Seperti yang dicatat dalam Ref. [ 33 ], tingkat keterlibatan tersebut tidak selalu diketahui sebelumnya, itulah sebabnya metode QM/MM adaptif dapat sangat berguna dalam mengeksplorasi efek ini.

3.2 Ketergantungan Ukuran Wilayah QM (cQM/MM dan adQM/MM)
Berbagai metode telah diusulkan untuk mendefinisikan wilayah QM [ 7 , 26 , 28 , 29 ], dan dalam karya ini, kami mengadopsi penugasan wilayah QM sferis langsung di mana struktur solvasi zat terlarut cQM/MM menentukan ukuran wilayah QM yang digunakan (rincian lebih lanjut dapat ditemukan di Tabel S4 , Gambar S3 dan S4 ). Untuk sistem Ala, wilayah QM pertama yang dipertimbangkan adalah “cQM/MM,” di mana hanya zat terlarut yang diperlakukan dengan metode QM, dan semua molekul pelarut diperlakukan dengan metode MM. Yang kedua adalah “adQM/MM(1),” di mana zat terlarut dan 6 air ditugaskan ke wilayah aktif (QM penuh), dan 15 air ditugaskan ke wilayah transisi (QM sebagian). Yang ketiga adalah “adQM/MM(2),” di mana zat terlarut dan 21 air berada di wilayah aktif dan 48 air berada di wilayah transisi. Batas untuk kulit solvasi ketiga adalah jarak di mana densitas pelarut cocok dengan densitas bulk. Untuk sistem Asp, ada dua definisi kulit solvasi, satu yang mencerminkan sistem Ala (Tabel 2 , Kulit 1, 2, dan 3) dan yang lain yang memperhitungkan minimum lokal kecil dalam RDF pada ~6,7 Å (Gambar S4 ). Kulit definisi kedua (Tabel 2 , Kulit 1, 2, 3*, dan 4*) selanjutnya akan dinotasikan dengan tanda bintang (*). Kami mempertimbangkan lima ukuran wilayah QM untuk sistem Asp secara total: cQM/MM (A = 0, T = 0); adQM/MM(1) (A = 7, T = 13); adQM/MM(2) (A = 20, T = 45); adQM/MM(2*) (A = 20, T = 22); dan adQM/MM(3*) (A = 42, T = 23). adQM/MM(2) dan adQM/MM(3*) hanya berbeda dalam proporsi molekul pelarut yang diperlakukan secara permanen dengan metode QM. Rincian lebih lanjut tentang ukuran wilayah QM yang digunakan dalam penelitian ini dapat ditemukan di Tabel S1 .

TABEL 2. Ukuran wilayah QM: Jumlah molekul pelarut dalam kulit solvasi cQM/MM dari Ala dan Asp a .
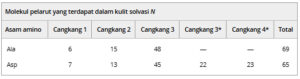Jumlah molekul pelarut yang terkandung dalam setiap cangkang menurut integral bulat dari fungsi distribusi radial ke minimum pertama, minimum kedua, dan minimum ketiga untuk sistem Ala. Sistem Asp dapat dianggap dengan cara yang sejajar dengan sistem Ala, atau cangkang keempat (4*) dapat didefinisikan mulai dari minimum lokal pada ~6,7 Å (yang juga menandai akhir dari Cangkang 3*). Total untuk cangkang Asp tetap identik terlepas dari definisi cangkangnya.
3.2.1 Ketergantungan Ukuran Wilayah QM pada Permukaan Energi Bebas
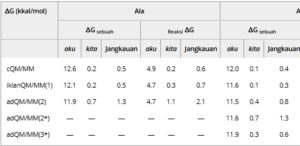
Kami menemukan bahwa profil energi bebas QM/MM secara kuantitatif serupa, terlepas dari partisi QM/MM yang digunakan. Energi bebas cQM/MM sedikit lebih tinggi daripada energi adQM/MM. Ketika data agregat dari semua replikasi dipertimbangkan, kurva yang dihasilkan (Gambar 2 ) untuk semua perlakuan adQM/MM tumpang tindih kecuali adQM/MM(3*) dari sistem Asp. Energi bebas aktivasi berkurang sekitar 0,5 kkal mol −1 ketika pelarut proksimal diperlakukan pada tingkat QM, dan efek pada energi bebas reaksi konsisten tetapi kurang jelas.
GAMBAR 2
Buka di penampil gambar
Kekuatan Gambar
Potensi profil gaya rata-rata reaksi tautomerisasi ala dan asp dengan berbagai ukuran daerah qm (Lihat Tabel S1 untuk detail tambahan). (A): PMF sistem Ala saat diolah dengan potensi cQM/MM (garis hitam pekat), potensi adQM/MM(1) (garis hijau putus-putus), dan potensi adQM/MM(2) (garis biru putus-putus). (B): PMF sistem Asp saat diolah dengan potensi cQM/MM (garis hitam pekat), potensi adQM/MM(1) (garis hijau putus-putus), potensi adQM/MM(2) (garis biru putus-putus), potensi adQM/MM(2*) (garis biru tembus pandang putus-putus), dan potensi adQM/MM(3*) (garis ungu tembus pandang putus-putus).
Statistik replikasi individual menunjukkan peningkatan deviasi standar dengan peningkatan ukuran QM (Tabel 3 ); ini mungkin disebabkan oleh berkurangnya waktu pengambilan sampel untuk daerah QM adQM/MM(2) dan jumlah atom QM yang lebih besar. Meskipun demikian, nilai rata-rata energi bebas dari semua simulasi QM/MM berada dalam satu deviasi standar dari energi bebas yang terkonvergensi dengan baik dari adQM/MM(1), dengan pengecualian adQM/MM(3*) dari sistem Asp. Berdasarkan data dan biaya komputasi yang diperlukan (Gambar S4 ), kami menyimpulkan bahwa untuk reaksi model yang dipertimbangkan di sini, hambatan reaksi dan energi reaksi menunjukkan variasi terbatas sehubungan dengan ukuran daerah QM.

TABEL 3. Statistik ringkasan energetika reaksi bebas replikasi dengan berbagai ukuran wilayah QM a .
adQM /MM(2*) dan adQM/MM(3*) disertakan untuk sistem Asp. Waktu pengambilan sampel per jendela payung adalah 40 ps (cQM/MM), 40 ps (adQM/MM(1)), 10 ps adQM/MM(2), adQM/MM(2*), adQM/MM(3*). Analisis kami mempertimbangkan sepuluh replikasi dari setiap sistem (Ala, Asp).
3.2.2 Ketergantungan Ukuran Wilayah QM untuk Transfer Muatan
Analisis pergeseran muatan (CSA) telah diusulkan sebagai metode yang andal untuk menentukan residu atau molekul pelarut mana yang harus disertakan dalam wilayah QM dalam simulasi cQM/MM [ 28 ]. Kami telah mengambil bilangan koordinasi kumulatif per kulit untuk kedua sistem Ala dan Asp dan mendefinisikan QMR i sedemikian rupa sehingga setiap QMR mengandung n air terdekat serta zat terlarut (misalnya, QMR 1, Ala mengandung Ala dan 6 atom pelarut dengan jarak terpendek ke karbon alfa Ala). QMR i didefinisikan secara individual untuk setiap snapshot yang digunakan. Transfer muatan antara zat terlarut QM dan pelarut QM telah dihitung dengan pendekatan cQM/MM dan ketergantungannya pada ukuran QM ditunjukkan pada Gambar 3 .
GAMBAR 3
Buka di penampil gambar
Kekuatan Gambar
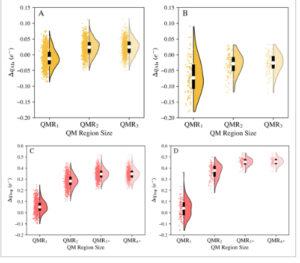
Pergeseran muatan dari zat terlarut QM ke pelarut QM dengan peningkatan ukuran wilayah QM berdasarkan cuplikan yang diambil dari simulasi cQM/MM. Panel (A, C): DFTB3/MM (1000 cuplikan); (B, D): B3LYP/6-31G*/MM (100 cuplikan). Plot ini menggambarkan perpindahan muatan dari zat terlarut QM ke pelarut QM di sekitarnya dengan QMR 1 : Kulit pertama, QMR 2 : Kulit pertama dan kedua, QMR 3 : Kulit pertama, kedua, dan ketiga untuk sistem Ala (kiri), dan kulit pertama, kedua, dan ketiga* untuk sistem Asp (kanan), dan QMR 4 : Kulit pertama, kedua, ketiga*, dan keempat* untuk sistem Asp. Lingkaran putih menunjukkan median perpindahan muatan dan kotak menunjukkan rentang interkuartil.
Muatan median yang ditransfer dari zat terlarut QM ke pelarut QM dalam kasus Ala ketika diolah dengan DFTB3 (Gambar 3A ) konvergen dengan penyertaan kulit solvasi kedua ke daerah QM, dan nilai absolut muatan median yang ditransfer tetap rendah pada kurang dari 0,03 e . Berdasarkan CSA, diharapkan bahwa adQM/MM(2) akan memberikan deskripsi yang memuaskan tentang efek transfer muatan dalam sistem Ala. Namun, sistem Asp melaporkan konvergensi yang lebih lambat (Gambar 3C ), di mana kulit tempat muatan yang ditransfer dari zat terlarut ke pelarut tidak lagi berubah ke depannya adalah kulit 3*, mungkin karena muatan bersih pada zat terlarut. Muatan median yang ditransfer antara Asp dan pelarut proksimal juga jauh lebih besar daripada Ala pada 0,35 e , dan ini diharapkan karena muatan pada rantai samping dan kemampuannya untuk didistribusikan melintasi pelarut proksimal. Untuk mempelajari apakah konvergensi yang lebih lambat tersebut berlaku pada tingkat teori yang lebih tinggi, analisis transfer muatan dilakukan lebih lanjut dengan B3LYP/6-31G*/MM. Kami menemukan bahwa terdapat jumlah muatan median yang ditransfer ke pelarut proksimal yang sedikit lebih besar (peningkatan 120 dan 140% untuk Ala dan Asp, masing-masing). Namun, tren yang sama diamati seperti pada perlakuan DFTB3 berkenaan dengan konvergensi transfer muatan. Berdasarkan analisis tersebut, tampaknya untuk memperoleh deskripsi konvergen dari efek transfer muatan berkenaan dengan ukuran QM, diperlukan adQM/MM(2), dan ukuran QM yang diperlukan lebih besar untuk perhitungan PMF.
CSA menyarankan bahwa tiga kulit harus disertakan dalam wilayah QM, tetapi hanya 1,5 kulit (deskripsi adQM/MM(1)) yang diperlukan untuk konvergensi energetika reaksi.

4 Kesimpulan dan Arah Masa Depan
Simulasi QM/MM gabungan memainkan peran penting dalam pemodelan multiskala dan simulasi sistem molekuler [ 63 – 65 ]. Upaya baru-baru ini telah dikhususkan untuk mengatasi beberapa masalah teknis utama yang membatasi akurasi dan penerapannya [ 1 , 2 , 66 , 67 ]. Pekerjaan saat ini berfokus pada dua masalah: yaitu, efek pengambilan sampel konformasi dan variasi ukuran wilayah QM; ini telah diatasi dengan sistem model dan metode simulasi QM/MM yang efisien. Hal ini memungkinkan kami untuk secara sistematis membandingkan kalkulasi reaksi berbasis minimisasi energi QM/MM dan simulasi PMF yang lebih mahal (Gambar S5 ). Hasil kami menunjukkan bahwa sangat penting untuk memasukkan fluktuasi termal dalam simulasi kinetika enzim, dan bahwa PES sangat bergantung pada struktur yang digunakan untuk kalkulasi energetika reaksi, konsisten dengan temuan sebelumnya [ 5 ]. Seringkali, ketergantungan tersebut bukan karena subsistem reaktif atau lingkungan langsungnya, yang mengaburkan interpretasi. Di sisi lain, untuk sistem model yang dipelajari di sini dengan metode QM/MM yang dipilih, kami menemukan bahwa energetika reaksi (baik hambatan reaksi dan energi reaksi) tidak terlalu sensitif terhadap ukuran wilayah QM, konsisten dengan hasil literatur [ 8 , 25 ]. Namun, kami mencatat bahwa muatan yang ditransfer dari zat terlarut ke lingkungan sekitarnya konvergen lebih lambat daripada energetika reaksi. Hal ini konsisten dengan penyelidikan sebelumnya yang menemukan bahwa konvergensi tergantung pada sifat molekuler mana yang sedang diselidiki [ 3 ]. Hal ini menyoroti pentingnya perhitungan pembandingan yang cermat untuk sistem yang diminati.

Perkembangan terbaru dalam metode simulasi QM/MM adaptif telah memungkinkan simulasi sistem difusif yang akurat termasuk transfer proton jarak jauh [ 34 , 68 , 69 ]. Bila digabungkan dengan metode QM semi-empiris yang efisien [ 31 , 70 ] atau implementasi GPU yang efisien dari metode DFT [ 48 ] dan ab initio [ 71 ] untuk deskripsi QM dan polarisasi elektronik eksplisit untuk deskripsi MM [ 72 ], ini akan menjadi alat yang ampuh untuk mempelajari ketergantungan ukuran QM sambil memperhitungkan fluktuasi termal dan memungkinkan pengambilan sampel konformasi yang memadai.